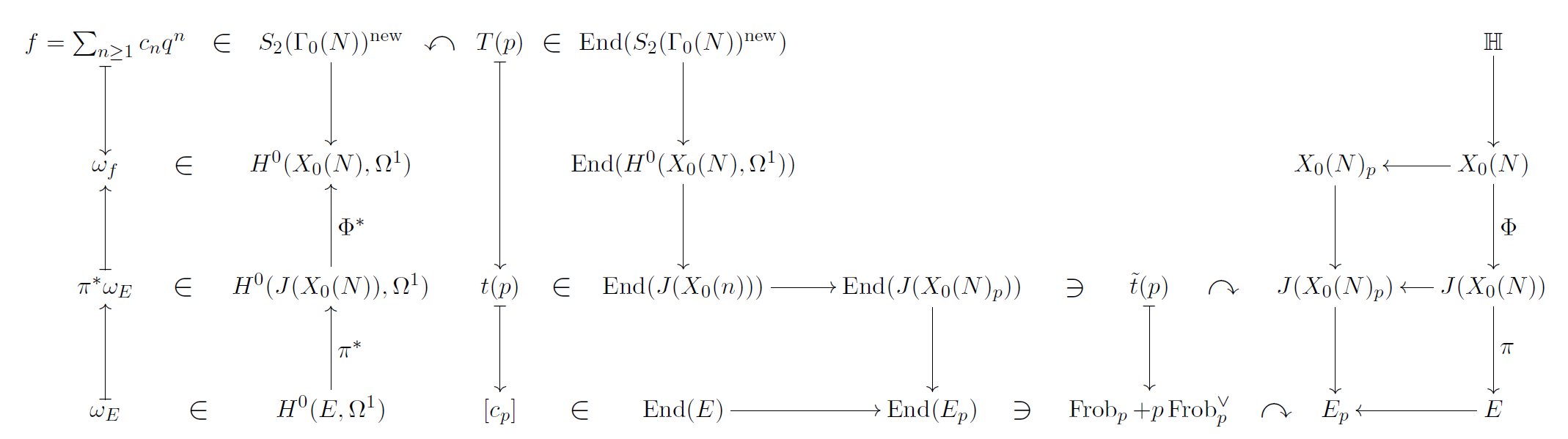Sam Mundy

5th year graduate student at Columbia University. My advisor is Eric Urban.

Past Seminars

Seminar on the Proof of Local Langlands (2019)

Local Langlands Seminar (Spring 2018)

Hida Theory Seminar (Fall 2017)

Shimura Varieties Reading Group (Summer 2017)

Algebraic Number Theory Meetings (Spring 2016)

Some papers

Eisenstein Series on Reductive Groups. These are handwritten notes for my lectures on Reductive groups and the constant terms of Eisenstein series, given in the seminar on analytic number theory at Columbia in the spring of 2019.

Here is my senior thesis (45 pages). The last section contains a new adelic proof of the Riemann-Roch Theorem for number fields.

Here is a link to my paper on this proof on the arXiv (8 pages).

Local Compactness and Number Theory: These are the notes for a seminar course (Math 639 Section 001) which I taught at UNM in the spring of 2015.

Here is a diagrammatic "statement" of the Eichler-Shimura Theorem for weight 2 modular forms. I have this printed on a coffee mug.

Tiny version:

I have a blog about extreme metal, and a math blog.

I walked from NYC to Boston during the summer of 2018.

Sam's email address is: sam@mundy.net